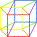
À partir d'un carré de côté a, une projection orthogonale de a engendre un cube.
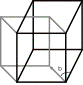		À partir du même carré de départ nous pouvons choisir une autre direction et trouver un autre cube.   Ces deux polyèdres nous paraissent orthogonaux, donc cubes. Ils sont séparés cependant par l'angle b de rotation de la translation. Entre les deux carrés d'arrivée, nous pouvons fermer ce module.
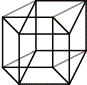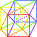
		Nous appelons ce résultat K3  ou  "le Cube au cube".   Tous les segments de cette représentation sont égaux. Elle n'est possible que si leur norme est unitaire. Tous les angles sont orthogonaux et supposés temporels. Déchiffrons K3 dans une lecture faite à partir du point fixe de notre vision.
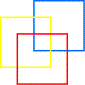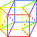
		Une des trois couleurs primaires est donnée à chacun des trois carrés, bases de nos trois cubes.

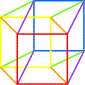		Les trois couleurs primaires sont reliées par leurs correspondantes secondaires.   > Les trois cubes du cube au cube K3
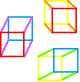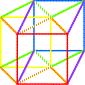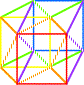
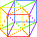
		K3 et le quatrième cube:   LA TOUR > le carré jaune forme un plan diagonal.
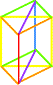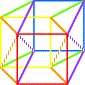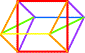
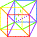
		K3 et le cinquième cube:   LE BERCEAU > le carré rouge forme un plan diagonal.
		K3, le 4° et le 5° cube:   LE HAUT FOURNEAU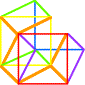
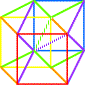		K3 et le 6°cube:   LE LIVRE > logiquement, le carré  bleu fait à son tour un plan diagonal. > les deux bases se sont rejointes en un point de reliure.
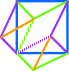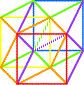		LA  TOTALE: tous les sommets des 3 carrés de départ sont reliés deux à deux. > le 7°cube:   LA VALISE    et son contenu.
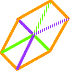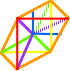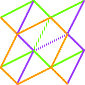		8° cube:  L'AILE VOLANTE > en enlevant les trois carrés primaires.   Rappel : Tous les segments sont égaux,                Tous les angles sont droits.
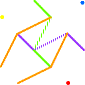		9° cube: LE SCARABÉE   > en enlevant les complémentaires de K3
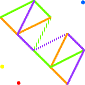		10° cube:  LES LUNETTES > ou "le cube miroir"
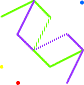		11° cube:  L'ÉOLIENNE > en enlevant l'orange du 10°cube Les mauves tournent vers la gauche. Les verts tournent vers la droite.
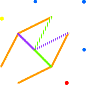		12° cube:  LE ROSSIGNOL > Impression de perspective. Le chant (pointillé) serait un symétrique du point visé (en haut à droite)... la note bleue
		13° figure:  LA VOIE LACTÉE > Les oeufs de Grenouille. Sommes-nous encore à égalité et orthogonalité des segments? Il n'y a plus de segments, donc de cube, mais l'espace est dimensionné.

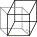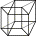		CODA Le cube au cube et son développement par les primaires.
		Fugue de cubes
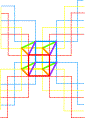
		Trame des points primaires > Une troisième dimension (profondeur)    donnerait une meilleure idée de cette  structure. > La trame des points secondaires n'existe pas, ou est sur la même grille
		Trame des primaires > Un plan à trois profondeurs.
		Trame des secondaires > Un autre angle de vue changerait l'angle de cette  trame,    jusqu'à obtenir des droites  perpendiculaires. > Noter les nids d'abeilles
		Plan de cubes au cube
		L '  H E P T A G O N E   M A G I Q U E
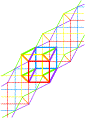
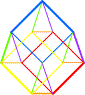
		C O N S T R U C T I O N     R A T I O N N E  L L E Sur un plan, 72 petits carrés (8x9)a inscrivent 90 points où sont élus 12 centres inscrits alignés sur 4 étages en  2 5 4 1
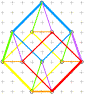		Sur  ces 12 points s'inscrivent les 3 cubes de K3 dans un heptagone magique   Heptagone: polygone à 7 côtés
		Quelle étrange maison ou est-ce une araignée?
		Est-ce la jupe d'Isabelle ou de grandes montagnes?
		L'oiseau ou le lutrin
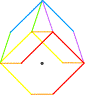		La maison de l'oiseau > Ce qui n'est pas à l'oiseau mais le contient
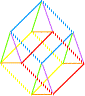		Les tréteaux pour la fête... > en comptant bien il y en a huit
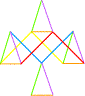		Mais n'est-ce là un Ange? > Retable de l'Hôtel Dieu à Beaune    peint en 1440-50 par Rogier de la Pasture    dit van der Weyden (1400 -1464)
		Ce qui est ni à l'Ange ni à la maison a mais spécifiquement à l'oiseau
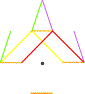		Ce qui n'est pas à l'oiseau a mais qui est à l'Ange et à la maison > Le chef d'orchestre
		Ce qui est ni à l'oiseau ni à l'Ange a mais spécifiquement à la maison
		Ce qui est ni à la maison ni à l'oiseau a mais spécifiquement à l'Ange
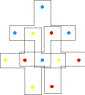		Les 3 carrés primaires dessinent sur les 12 points 3 croix a incluant chacune la paire opposée
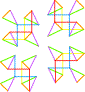		L'envol des Archanges a Gabriel                   Raphaël                                     Uriel                                                   Mikaël
		Quatre Anges réunis au même point a le Big-bang le lac la nappe sur le pré
		La plus simple des manières de dessiner notre figure est de partager les côtés d'un carré en cinq parties.
		Le prisme dévie la lumière en un faisseau de couleurs.   Un rayon lumineux en abscisse, un rayon lumineux en ordonnée, nous donnent le carré  incluant notre figure.
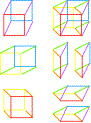		PRÉCISIONS   En 2000, HMS Coxeter m'a précisé que K3 est un double prisme ou produit rectangulaire (cartésien) entre un carré et un triangle.   Dans ma lecture de K3, je n'ai pas pris en compte les prismes entre 2 triangles (les tréteaux) pensant qu'il s'agit du déplacement d'un cube à un autre. J'investissais les prismes en tant que quatrième dimension, la dimension temporelle reliant les trois cubes. En fait, K3 est un polytope comprenant 3 cubes mais aussi 4 prismes.   Ce n'est pas un hypercube qui comporte 8 cubes, mais c'est un polytope de 7 espaces {4}x{3} que j'ai baptisé "Hippocube" pour sa ressemblance avec la race des équidés.

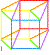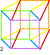
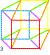
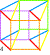
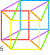
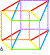
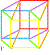
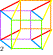
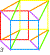
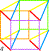
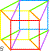
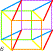
		Les douze chevaux   12 manière de peindre K3 avec un cercle des couleurs dextrogyre 1 2...   et levogyre 1' 2' ...
		AVEC 4 CARRÉS
		Reliant 4 carrés par 4 carrés   Représentation de l'hypercube C8 où chaque face est commune à 2 cubes et chaque sommet a 4 arêtes (4D). On peut lire 8 cubes dans un octogone.
		Voir: "Huit navires portant chacun trésor"
		AVEC 5 et n CARRÉS
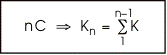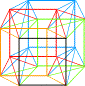		"L'hippocube à base de n carrés contient un nombre de cubes égal à la somme des entiers de 1 jusqu'à n-1 "
		LE TRICUBE PAR LES SURFACES