 |
«J'AIME ALICE, DONC
ALICE MÊME» |
Propos sur
l'hyperespace
par Antoine WALTER Publié dans la revue L'OUVERT IREM - Strasbourg - Avril 2001 |
||
|
D'abord j'étais
luthier, je construisais des violons et réfléchissais
au style. Quand on s'appelle Antoine et que l'on est
confronté à Antonio Stradivarius, Nicolo Amati,
Domenico Montagnana, Jean-Baptiste Vuillaume et autres
maîtres de la transformation du bois en instruments de
musique, on se demande pourquoi de telles merveilles?
Comment cela se fait-il, comment cela s'écrit-il, le
fait d'appliquer à un matériau (érable, épicéa, ébène)
un art tel qu'il transporte les gens pendant des
siècles, qu'il pousse à l'admiration tant pour les
yeux que pour les oreilles toute âme sensible et prête
à l'émerveillement.
C'est un problème de style, soutenu dans son histoire, un problème de situation dans le monde, un problème d'économie du geste et de la pensée, un problème spécifiquement de langage et de relation dimensionnelle. Plus loin, je travaillais le violoncelle. Là aussi, émission sonore, on pourrait dire physique, et réceptivité spatiale sont au coeur de la recherche. Comment passer du point de contact entre corde et archet à l'espace? Comment passer du signifiant, la note écrite à la phrase dite? Comment passer de la pulsion à l'oeuvre, de l'ennui et du désoeuvrement à la joie, de l'inconscient au conscient? C'est là le travail de l'artiste que de laisser advenir les ordres cachés de son désir et de les mettre en jeu dans la représentation. Qu'elle soit fantasmatique, plastique, picturale ou modélisable, musicale, algébrique ou géométrique, cette représentation use des outils du langage. Parfois elle cherche plus loin à inventer d'autres outils pour explorer de nouvelles régions, ou à donner de nouveaux sens au commun de la métaphore. Le patient travail d'élaboration de la pensée, d'architecturisation du monde, de mise en ordre des figures, d'harmonisation des concepts, va de paire avec un travail de deuil sur les idées reçues et sur la trame des résistances. La figure est pointée par son existence même. L'artiste pointe la représentation qu'il fait de l'accès à son désir où se réfléchissent les mille facettes de la figure. Elle n'en reste pas moins toujours plus loin et toujours au-delà. Nous voilà dans le style et dans la limite. Le style en tant qu'enchaînement des signifiants, la limite dans la nomination et la représentation même. Aimer Alice, aimer la figure, c'est entrer dans son existentialité et dans son mystère, dans le sens qui se dégage de ses traits, dans la cohérence qu'elle invite à suivre. C'est une bonne position pour être un artiste, aussi scientifique que possible, inscrit sur les fibres de la vérité qui de toute façon restera mi-dite, voilée dans l'étrangeté de l'Être et l'altérité de l'Autre. |
| Ma
première
rencontre visualisée avec l'hyperespace a été un dessin
très simple:
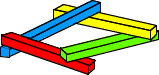
Trois carrés
reliés entre eux forment trois cubes.
 J'ai passé une dizaine d'années à tourner et retourner cette chose mystérieuse sans trop savoir comment la ranger dans l'ordre des polyèdres et polytopes. Je l'appelais le cube au cube K3. J'y voyais plutôt une multiplication de 3 cubes entre eux qu'une addition qui aurait été 3 cubes juxtaposés. Je conjuguais ce dessin dans un petit livre intitulé "Histoire du carré", affublant chacun des 3 carrés d'une couleur primaire, la couleur secondaire correspondante formant la liaison. J'appliquais toutes sortes de trinités à ces trois espaces topologiquement reliés: grâces mythologiques, Sainte Trinité religieuse, noeud borroméen lacanien RSI, etc. L'accueil de mes idées auprès des personnes que je rencontrais était très mitigé, souvent admiratif, étonné, dérouté. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Jacques Lacan, disant:"
L'inconscient est structuré comme un langage", a
schématisé la Psyché selon un noeud borroméen à 3
ronds, liant les trois registres fondamentaux: Réel,
Symbolique, Imaginaire.
La propriété borroméenne est liée au fait que la coupure d'un rond libère les deux autres. |
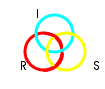 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
En 2000, je
rencontrais le professeur Nicolas Rivier de la faculté
de Physique des Solides, qui m'a beaucoup aidé à
préciser mes notions de l'hyperespace. Grâce à lui,
HMS Coxeter nous envoyait un mail disant de mon cube
au cube qu'il s'agit d'un double prisme ou produit
rectangulaire ou produit cartésien d'un carré et d'un
triangle.
Regular Polytopes
p.124 Regular Coxeter Polytopes
p.37
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
C'est un polytope
bien sûr, mais non régulier, puisqu'il y a des faces
carrées et des faces triangulaires. Entre les
triangles, il y a 4 prismes. Ces prismes témoignent du
passage d'un cube à l'autre. Ils sont l'angle de
rotation d'un cube à l'autre. On pourrait dire qu'ils
sont l'angle temporel si le temps est pris comme
quatrième dimension. En chaque sommet de K3, tous les
angles sont orthogonaux. Nous sommes dans la quatrième
dimension, puisque en chaque sommet, il y a 4 arêtes.
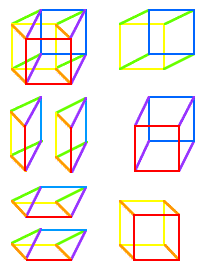
K3 n'est pas un hypercube qui comporte 8 cubes, mais c'est un polytope de 7 espaces {4}x{3} que j'ai baptisé Hippocube pour sa ressemblance avec la race des équidés.  La modélisation
de K3 en 3D m'a longtemps posé problème. La modélisation
de K3 en 3D m'a longtemps posé problème.Alors qu'en 2D la représentation en perspective cavalière nous paraît orthogonale, et qu'elle est strictement orthogonale en 4D, la 3D oblige à tronquer 2 cubes en parallélépipèdes. |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Construction et évolution de K3 : - Carré - Cube - 2 Cubes - 3 Cubes - 3 Carrés - K3 - la Tour - le Berceau - le Haut-Fourneau - le Livre - la Totale - l'Aile Volante - les Lunettes - l'Éolienne - le Scarabée - le Rossignol - la Voie actée Lire le tableau comme suit :  |
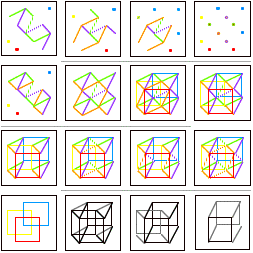 Voir: Histoire du Carré |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Plus loin, je
regardais les gravures d'Escher. Comment faisait-il
pour évoquer sur son dessin des espaces tellement
difficiles en 3D? Je trouvais une solution en donnant
une épaisseur aux arêtes du plan et en les superposant
dessus-dessous. Cela formait des plans hélicoïdaux qui
pouvaient être soit lévogyre, soit dextrogyre.
J'apprenais que l'espace courbe est orienté.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
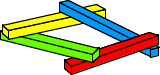 Plan lévogyre
|
 Plan dextogyre
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Un cube eschérien a 6 faces hélicoïdales orientées dans le même sens. L'étude des symétries à l’aide de couleurs y est intéressante. Donnant à chaque hauteur une couleur, il y aura une largeur et une profondeur de même couleur en symétrique du barycentre. Au fur et à mesure que l'on resserre le cube sur lui-même tout en gardant l'épaisseur des arêtes, la courbure de l'espace augmente. Il arrive un moment où les 12 arêtes du cube forment un entrelacs symétrique de 4 triangles, dont les sommets sont inscrits dans un cuboctaèdre. Chaque hauteur, largeur, profondeur de même couleur se sont rejointes en un triangle équilatéral. Pour ceux qui se sont intéressés à la théorie des noeuds, les sommets d'un cube eschérien sont des triskels. Ses faces sont des quadriskels. Pour le tétraèdre, sommets et faces sont des triskels. Pour l'octaèdre, sommets quadriskels, faces triskels. De plus sommets et faces ont un sens alterné: quelque soit le polyèdre, si ses faces sont lévogyres, ses sommets seront dextrogyres. |
  |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Dans l'espace eschérien, il s'agit d'une courbure des directions de l'espace qui n'est pas encore de l'hyperespace. C'est de la 3D courbée telle qu'Einstein le montre avec la relativité aux abords des très grandes masses et de la vitesse de la lumière. L'Hyperespace en tant que tel demande une gymnastique de l'esprit un peu particulière. C'est que nous sommes très habitués à réfléchir et à nous représenter le monde cartésiennement avec trois dimensions: largeur, hauteur, profondeur. La première idée pour symboliser une 4° dimension est de dire que c'est du temps. C'est la position de la physique newtonienne. Faire de cette idée de temps une idée de géométrie spatiale, voilà la difficulté. Et pourtant, nous y sommes tous les jours invités. Le chant d'un oiseau qui brise le silence et traverse l'espace, c'est une quatrième dimension. Un tableau dans une chambre change l'atmosphère et l'espace s'en trouve recentré ou dispersé, oppressé ou agrandit. Un musicien fait vibrer à travers l'espace de la salle celui de son violon, de la musique qu'il interprète, de l'époque qu'il met en jeu dans la situation présente. En fait toute irruption du langage dans le monde me paraît comme une invitation à l'hyperspacialité. Comment
s'échafaude les lieux des dimensions entre elles?
J'ai souvent remonté l'échelle de ce qui est apparent, bien connu de nos consciences: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Cela demanderait
de long développements qu'il n'est pas utile de faire
ici.
Mais pour comprendre spécifiquement l'hyperespace, essayons de penser le bord de ces dimensions. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Un hyperespace n'est
absolument pas un objet 3D. Ce que l'on peut représenter
en 2 ou 3D sont des projections, tout comme un plan
d'architecture qui n'est pas la maison même, ou une
carte du Club Vosgien le Ballon d'Alsace. Edwin Abott en
1884 écrivait un livre intitulé ''Flatland'', où il
raconte l'existence d'êtres vivants en 2D, sur des
plans. Le narrateur y est un carré et se demande ce que
pourrait être Spaceland. Nous sommes des êtres de
Spaceland pour Hyperspaceland. Pour se représenter mentalement un hypercube, il faut penser un cube bordé par des cubes chacun bordé par des cubes, sachant qu'il y a seulement 8 cubes dans un hypercube, et non un remplissage de l'espace 3D par des cubes. Le bord de l'hypercube est toujours un cube. Si l'on s'imagine être dans un cube, il y aura un cube devant, un derrière, un à droite, un à gauche, un au-dessus, un en-dessous, cela fait 6 cubes autour de nous, plus celui où nous sommes: 7. Le huitième cube bordera les cubes de telle sorte que quel que soit le cube où l'on se trouve, il y en aura toujours un devant, un derrière, un à droite, un à gauche, un au-dessus et un en-dessous. Il faut que l'espace devienne mou comme chez Dali, qu'il se relativise comme chez Einstein, qu'il se poétise comme chez Rimbaud et on rentre dans la 4D comme un yogi tout à fait relaxé. Il est étonnant de sculpter une pierre, parce qu'on doit toujours en enlever, et il est étonnant de pousser son esprit vers l'hyperespace parce que toute notre gloire cartésienne y est intrinsèque et ne cesse d'y demeurer. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
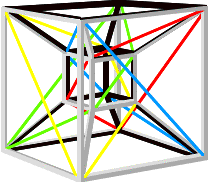
Projection centrale d'un Hypercube quadridimentionnel dans l'espace à trois dimensions avec en couleurs les fibres de Hopf Voir: Huit Navires portant chacun trésor et la rose de l'Octogone |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Penser les
polytopes réguliers de la 4° dimension ne peut se
faire sans passer par l'hypersphère S3. Tout comme un
polyèdre est la solidification de la sphère S2 dans
R3, un polytope sera la solidification de
l'hypersphère S3 dans R4.
La fibration de Hopf donnant le sens de l'espace courbe permet d'inscrire les sommets du polytope sur une grille ressemblant à des méridiens sur S2. Sur S3 les fibres de Hopf sont des parallèles courant sur les 3 tores dans R3 ou sur l'hypersphère dans R4. Coordonnées euclidiennes de S3 dans R4: x2 + y2 + z2 + t2 = r2 N.B: Le rayon de S3 est un carré! |
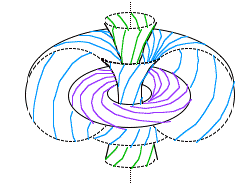 Fibration de Hopf de S3 représentée par projection dans R3 (cf. JF Sadoc: La frustration géométrique) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
L'hélice de
Coxeter est un empilement de tétraèdres qui rend bien
compte de la nature de ces fibres structurant l'espace
courbe.
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Je me suis rendu
compte par hasard qu'en inversant la chiralité (le
sens de la courbure) tous les 6 tétraèdres, on
obtenait une roue tétraèdrique plane de 96 tétraèdres:
32 fois 3 tétraèdres formant un bateau: |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
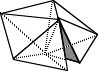
Plastiquement,
cette roue se ferme bien.
Mathématiquement, il y a cependant un trou angulaire de 6° 36' 11". Voir: Polyèdres La roue de 5 tétraèdres nous avait déjà montré un angle de cette nature. Il a été nommé par J.F. Sadoc, lors de son étude des symétries de l'Icosaèdre et des structures moléculaires de dim 4: la frustration géométrique. Il s'agit là d'une porte qui mène de l'icosaèdrisme (structures basées sur le polyèdre régulier le plus proche de la sphère: l'icosaèdre) vers l'espace courbe quand les tétraèdres non réguliers de l'icosaèdre deviennent réguliers. |
  |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
C'est par un
manque que la structure s'ouvre, comme dans le cycle
des tonalités musicales, un manque qui fait la
vibration de la musique, l'élan du discours, la source
du désir. L'imperfection de la 3D mène vers un monde
plus vaste et plus conscient, où le cartésianisme est
intrinsèque.
C'est le passage qu'explore Alice vers les lieux de son rêve.  Ô saisons, ô châteaux, Quelle âme est sans défauts ? Antoine Walter 13 mars 2001 |
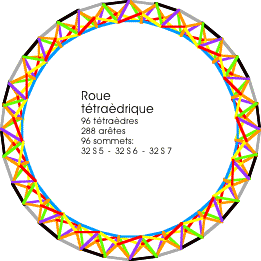 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tableau des 5
Polyèdres réguliers dans R3 et des 6 Polytopes réguliers
dans R4 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Article
publié
dans la revue L'OUVERT - IREM - Strasbourg - Avril
2001
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| >>
ADVENTUM: Proposition et
Hypothèses 2006 >> TOPOS 2021 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||